Cuando se nos plantea un problema, una de las cosas que hacemos a menudo es dividirlo en trozos más simples. Esta estrategia suele ser buena por varias razones: una es que las partes suelen ser más fáciles de resolver que el problema entero y, la otra, que a veces resolviendo tan solo alguna de ellas llegamos a una solución satisfactoria para el total. Es una aplicación del famoso “divide y vencerás”.
En la empresa, segmentar es una manera de dividir un problema en partes más sencillas que ayuda a priorizar esfuerzos y a localizar oportunidades de negocio. No todos los clientes son iguales ni tienen las mismas necesidades. Por tanto, las compañías deben entenderlo y adaptar sus propuestas de valor a cada grupo objetivo. Segmentar es dividir una población en grupos homogéneos en función de necesidades, comportamientos, características o actitudes y caracterizar a los grupos resultantes para saber qué les distingue entre sí.
Una manera muy útil de segmentar y entender a qué tipo de población estamos estudiando es ver cómo se organizan sus individuos de forma natural. Para eso se utiliza el algoritmo k-means, uno de los más famosos de la ciencia de datos en general y para hacer clustering en particular.
Éstas son algunas de las preguntas que puede ayudar a resolver: ¿qué tipo de clientes tengo?, ¿cuáles son los que menos productos contratan?, ¿qué tiendas venden más (o menos) de lo que deberían?, ¿están bien ubicadas?, ¿cuáles son los clientes más sensibles al precio?…
El algoritmo de k-means es un sencillo método para dividir, en base a una serie de variables, una población en un número k de segmentos (o clusters) determinado por el usuario. El primer paso del algoritmo es la inicialización. Para ello se seleccionan k individuos de la población al azar. Esos individuos son los representantes de cada clúster y se llaman también centroides. Una vez hecho esto, el algoritmo repite un número de veces dos sencillos pasos:
- Asignación de individuos. Cada individuo se asigna al clúster a cuyo centroide está más cerca. Para ello se mide la distancia entre él y cada centroide. Una de las distancias más utilizadas es la euclídea. Esto genera una partición de los datos.
- Actualización de los centroides. El nuevo representante del grupo se traslada al centro (media) de todos los individuos asignados a él.
Estos pasos se repiten hasta que los grupos se mantienen iguales o, lo que es lo mismo, no hay nuevas reasignaciones de individuos en el paso 1: el algoritmo ha convergido.
Mi hijo y yo jugamos a veces a las cartas de Pokémon. Es un juego sencillo. Nos repartimos unas cuantas cartas del taco y cada ronda enfrentamos dos de ellas (una carta cada uno). Uno de nosotros comienza la batalla y el contrincante replica. Las decisiones se toman en función de las fortalezas o debilidades de los Pokémon que nos tocan. Los ataques van restando puntos de vida y al final de cada partida siempre hay un vencedor. Así jugamos él y yo. El que gana la batalla se lleva la carta del otro. Cuando yo era niño, había un juego parecido con coches de Fórmula 1, en el que las batallas eran más simples: el que lanzaba el ataque elegía una característica y si era mejor en ella que el coche del contrincante, se lo llevaba. Con los Pokémon las batallas se complican un poco pero la esencia es la misma. Hay dos cosas fundamentales que pueden ayudar a ganar una partida: tu pericia como jugador a la hora de manejar la batalla y la suerte que tengas con las cartas que te tocan. A veces, por muy bueno que seas, no tienes nada que hacer si las cartas de tu contrincante son mucho mejores que las tuyas, y esto pasa con cierta frecuencia. Con el análisis clúster podemos reducir notablemente el factor suerte de los jugadores y dejarlo todo en manos de la pericia. Veámoslo.
En Internet hay datos abiertos de casi todo y los Pokémon no son una excepción. En esta página se encuentra el listado de la última generación Pokémon junto con sus características. En concreto, utilizaremos estas cuatro:
- HP: son los puntos de vida, que se van restando con los daños sufridos en la batalla.
- Attack: son los puntos que se utilizan para hacer daño físico al oponente.
- Defense: Son los puntos con los que se defiende de un ataque.
- Speed: Es la puntuación que define quién empieza la batalla.
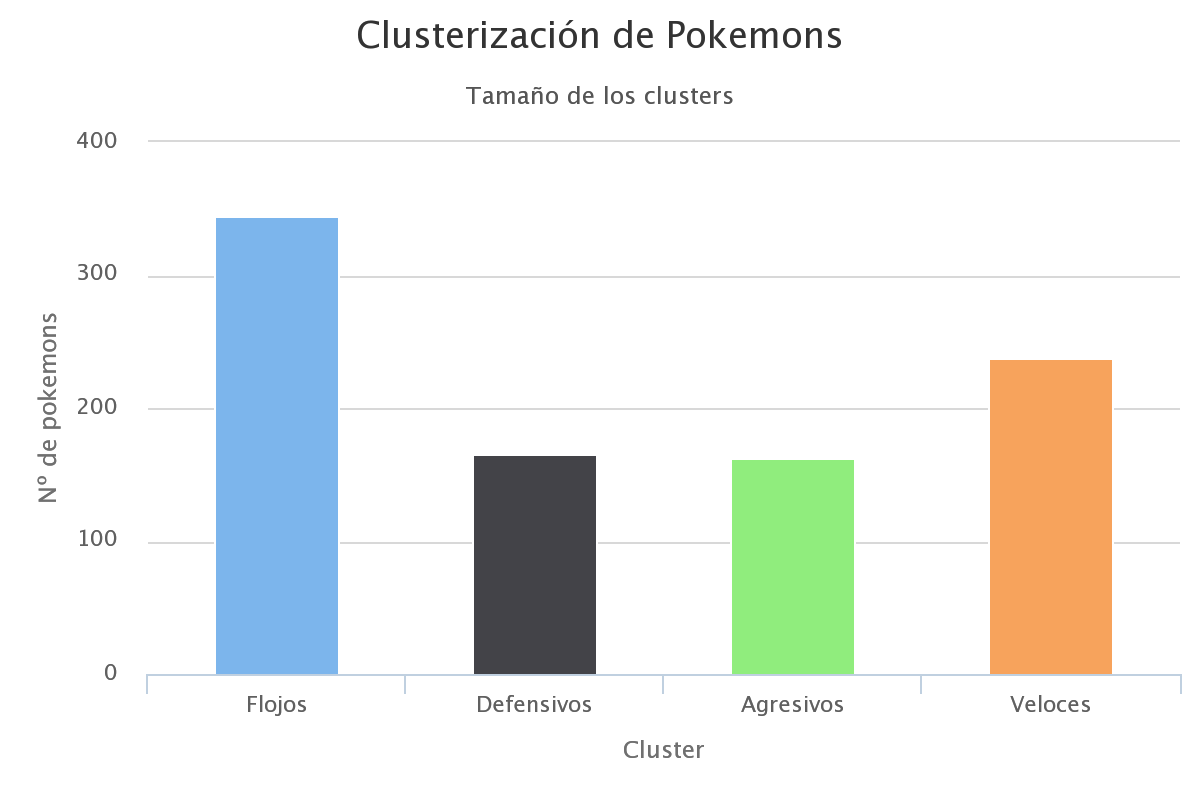
Con estas características podemos dividir a los 909 Pokémon en cuatro grupos bien diferenciados. Éste es el tamaño de cada grupo:
En la gráfica anterior habréis observado que hemos bautizado a los grupos como Flojos, Defensivos, Agresivos y Veloces. Para entender por qué, veamos las características medias de los individuos de cada grupo:
Los agresivos, por ejemplo, son los que mejor promedio de ataque y de puntos de vida tienen (son los que queremos tener mi hijo y yo cuando jugamos). Los defensivos son auténticas murallas. Es interesante ver cómo el grupo más numeroso son los flojos, que no destacan por nada en particular. Los veloces son un grupo interesante, porque dan a quien los tiene la posibilidad de comenzar la batalla, y eso es una ventaja importante.
Para poner cara a los grupos, veamos a un individuo representativo de cada uno
- Eevee, como representante de los flojos:
- Scrafty como representante de los defensivos:
- Swampert, como representante de los agresivos:
- Y Basculin, como representante de los veloces:
Podemos utilizar los grupos resultantes para minimizar el factor suerte en las partidas. Si repartimos ocho cartas, podemos hacerlo de dos maneras:
- Tomándolas al azar de todo el taco, como hacemos nosotros cuando jugamos
- Tomando dos cartas al azar de cada uno de los cuatro tacos
Esta segunda manera hace que las cartas sean más homogéneas entre los participantes. Una manera de verlo es simular repartos con ambos métodos y comparar la desviación típica de la suma de las características de los Pokémon repartidos. En concreto, si simulamos 5.000 repartos, estos son los resultados:
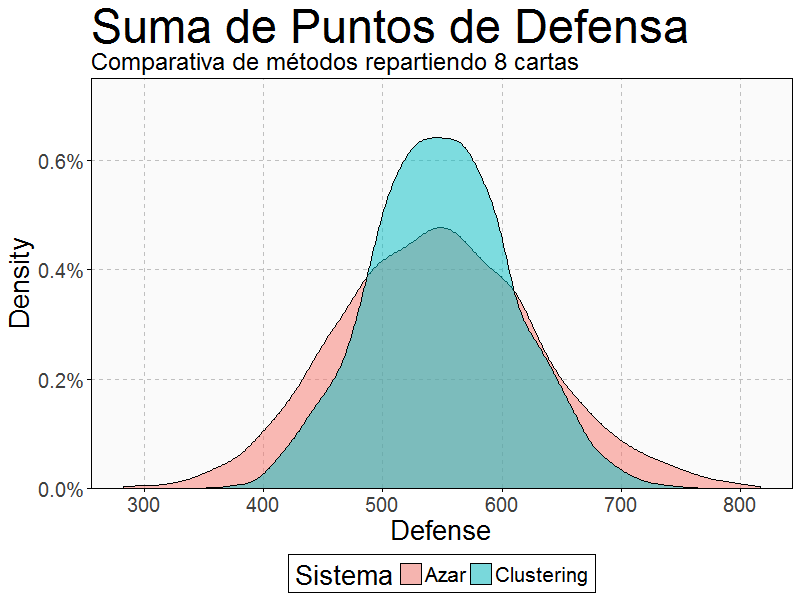
La desviación de todas las puntuaciones tomando dos cartas de cada grupo es significativamente inferior que la del primer método. Eso quiere decir que las cartas serán más comparables si usamos este método. Gráficamente se puede ver muy bien la diferencia. Por ejemplo, ésta es la distribución de la suma de los puntos de defensa de las ocho cartas repartidas según ambos métodos:
La distribución de los puntos generados por el método de k-means es más estrecha que la de los generados por el otro método. Es decir: tiene una varianza menor.
Para hacer todo el experimento (descarga y preparación de datos, ejecución del k-means y visualización de los resultados) he utilizado R. Si alguien quiere el código, sólo tiene que pedírmelo.
Gráficos: Antonio Sánchez Chinchón
Soluciones y Sectores
Te puede interesar
-
Edificios sostenibles para un turismo más inteligente y competitivo
El sector turístico representó el año pasado el 12,2% del PIB en España. Se trata, por tanto, de un ...
-
La capacitación en industria 4.0, condición sine qua non para su transformación
Recientemente leía un artículo sobre “Desafíos de la industria europea en la nueva coyuntura socioeconómica”. En él se apuntaba, ...
-
Hospitalización domiciliaria: un nuevo paradigma en la gestión de pacientes crónicos
Como explicaba en un post anterior, asistimos a la transformación de la atención médica para mejorar la calidad de ...
